Term (logic)
In mathematical logic, universal algebra, and rewriting systems, terms are expressions which can be obtained from constant symbols, variables and function symbols. Constant symbols are the 0-ary functions, so no special syntactic class is needed for them.
Terms that do not contain variables are known as ground terms; they are used to form ground expressions.
Terms in first-order logic are essentially defined this way.
Given a signature for the function symbols, the set of all possible terms that can be freely generated from the constants, variables and functions form a term algebra.
An expression formed by applying a predicate to a sequence of terms, whose length matches the arity of the predicate (or one of the allowed arities, in the case of a multigrade predicate), is known as an atomic formula. In bivalent logics, given an interpretation, this atomic formula will then be true or false.
Formal definition
A term may be defined as:
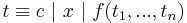 ,
,
That is, a term is recursively defined to be a constant c (a named object from the domain of discourse), or a variable x (ranging over the objects in the domain of discourse), or an n-ary function f whose arguments are terms tk. Functions map tuples of objects to objects.
References
- Franz Baader; Tobias Nipkow (1999). Term Rewriting and All That. Cambridge University Press. pp. 1–2 and 34–35. ISBN 9780521779203.